Imitation Learning: behavioral cloning

https://zhuanlan.zhihu.com/p/68818193

行为克隆问题定义

给定一组由专家策略 $\pi_E$ （策略未知）生成的示范数据（训练数据集）$D = \{{tr_i}\}_{i=1}^m$，其中

1. 每条轨迹 $tr_i = {s_1, a_1, s_2, a_2, \ldots, s_H, a_H}$

2. $s_j$ 表示状态，$a_j$ 表示动作，$H$ 表示轨迹长度

模仿学习的目标是学习一个策略 $\pi_\theta$ ，使其尽可能接近专家策略 $\pi_E$。

基本流程：先获取专家数据（训练用），然后以 $o_t$ 作为输入，产生的动作 $a_t$ 作为输出（标签），通过监督学习的方法进行训练

目标： $\max _\theta \mathbb{E}_{o_t \sim p_{data}(o_t)}[\log \pi_\theta(a_t|o_t)]$，其中 $p_{data}(o_t)$ 表示训练（专家）数据分布， $a_t$ 为专家动作，故该式表示在 $t$ 时刻选择正确动作的对数概率的期望

行为克隆数学推导

考虑已有的数据集 $D$，如何恢复专家策略 $\pi^E$ 呢？

行为克隆的想法很简单，我们直接从数据中估计 $\pi^E$。 一个经典的估计方法就是极大似然估计：对于数据集中每一个状态-动作对 $(s,a) \in D$，希望最大化策略 $\pi_\theta$ 在状态 $s$ 下选择动作 $a$（专家） 的概率：

从轨迹的角度考虑，一条完整轨迹的概率可以表示为：

取对数后：

在行为克隆中，我们关心的是策略 $\pi_\theta$，而初始状态分布 $\rho(s_1)$ 和状态转移概率 $p(s_{t+1} | s_t, a_t)$ 与策略参数 $\theta$ 无关。因此，最大化对数似然等价于最大化与 $\theta$ 相关的项：

这与先前从状态-动作对角度得到的优化目标是一致的

对于离散动作空间，公式 (2) 的最优解可以通过“计数”来求解，$\pi_\theta(a|s) = \frac{N(s,a)}{N(s)}$，其中 $N(s,a)$ 是状态-动作对 $(s,a)$ 在数据集中出现的次数，$N(s)$ 是状态 $s$ 出现的次数；对于数据集里没有出现过的状态 $s$，可以令其动作分布为一个均匀分布，即 $\pi(a|s)=\frac{1}{|A|}$，其中 $|A|$ 为动作空间的大小

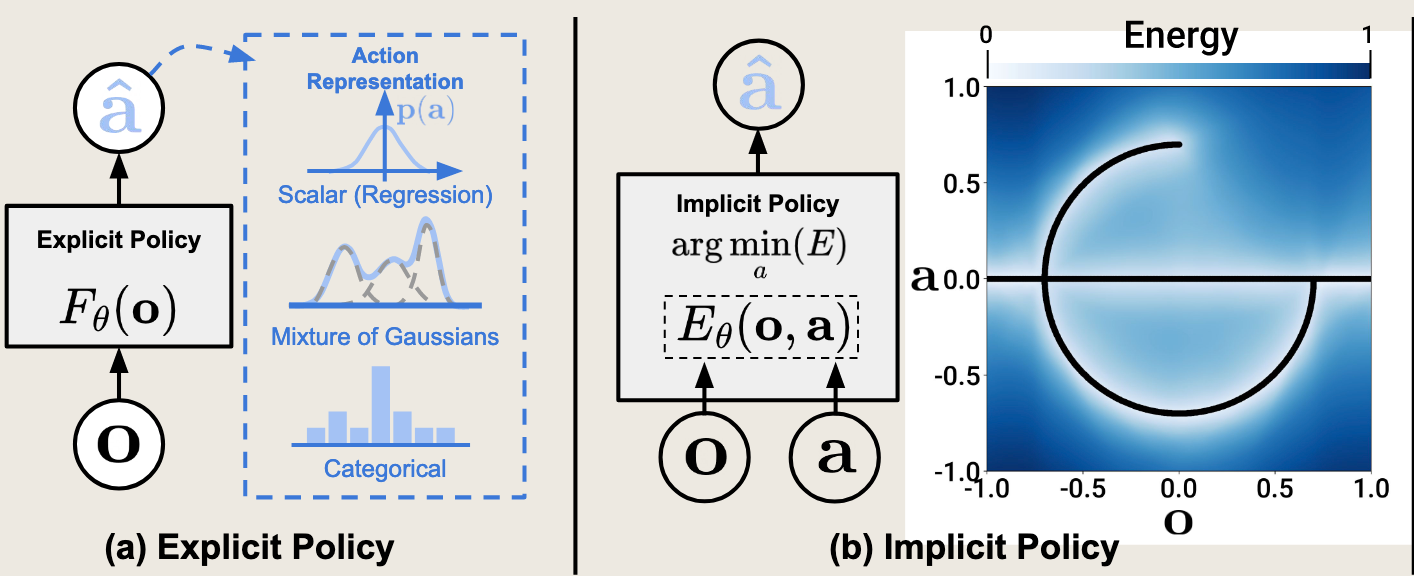
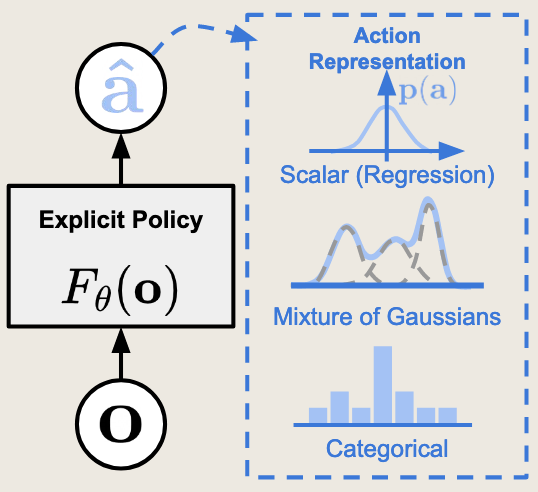
对于连续动作空间，可以使用高斯分布来表示策略。具体地，对于每个状态 $s$，我们将策略 $\pi_\theta(\cdot|s)$ 表示为高斯分布 $\pi_\theta(a|s) = \mathcal{N}(\mu_\theta(s), \sigma^2_\theta(s))$【参数化方法】

在参数化表示法中，高斯分布和神经网络扮演不同的角色：

1. 高斯分布是策略的输出形式：对于连续动作空间，我们通常用概率分布来表示策略 $\pi_\theta(\cdot|s)$，而高斯分布是一种常用的概率分布选择。它需要均值 $\mu$ 和方差 $\sigma^2$ 两个参数来定义。

2. 神经网络是函数逼近器：它用来生成高斯分布的参数。具体来说，神经网络接收状态s作为输入，输出高斯分布的参数 $\mu$ 和 $\sigma^2$

神经网络负责从状态映射到分布参数，高斯分布负责基于这些参数给出动作的概率密度

对于多峰问题，可以使用混合高斯分布来求解，即多个高斯分布叠加

行为克隆的分布偏移问题

训练阶段基于专家演示数据学习，对应状态分布 $p_{train}(s)$，测试阶段智能体面对的状态分布为 $p_{\pi_{\theta}}(s)$，两者不同产生分布偏移。下面分析：在给定策略犯错概率界限 $\epsilon$ 的假设下，分析学习到的策略 $\pi_\theta$ 对应的状态分布与训练集状态分布的差异

在深入探讨行为克隆的分布偏移问题前，先引入 KL 散度（Kullback-Leibler divergence）的概念，它在衡量两个概率分布的差异方面具有重要作用。KL 散度，也称为相对熵，用于描述两个概率分布 P 和 Q 之间的差异程度，其公式定义为： $D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}$
对于离散概率分布，x 取遍所有可能的取值；对于连续概率分布，则通过积分形式表示 。KL散度具有非负性，即
$D_{KL}(P||Q) \geq 0$，并且当且仅当 P = Q 时，$D_{KL}(P||Q) = 0$。直观来说，KL 散度值越大，表明两个分布的差异越大；值越小，则说明两个分布越相似。
在行为克隆中，我们常利用 KL 散度衡量学习到的策略分布与专家策略分布之间的差异，进而分析算法性能和策略优化方向。

原始形式推导

• 假设条件：假设在训练集 $\mathcal{D}_{train}$ 中，对于服从 $p_{train}(s)$ 分布的状态 $s$，学习到的策略 $\pi_{\theta}$ 采取非最优动作（与专家策略 $\pi^*(s)$ 不同的动作的概率不超过 $\epsilon$，即 $\pi_{\theta}(\mathbf{a}\neq\pi^*(s)|s)\leq\epsilon$

• 状态分布公式推导：定义 $p_{\theta}(s_t)=(1 - \epsilon)^t p_{train}(s_t)+(1-(1 - \epsilon)^t)p_{mistake}(s_t)$，其中，$(1 - \epsilon)^t$ 代表到时间步 $t$ 都不犯错的概率， $p_{train}(s_t)$ 是训练集中状态 $s_t$ 的分布，所以 $(1 - \epsilon)^t p_{train}(s_t)$ 表示到时间步 $t$ 都不犯错时状态 $s_t$ 的分布贡献；$1-(1 - \epsilon)^t$ 是到时间步 $t$ 至少犯一次错的概率，$p_{mistake}(s_t)$ 是犯错情况下状态 $s_t$ 的某种分布，$(1-(1 - \epsilon)^t)p_{mistake}(s_t)$ 是犯错时状态 $s_t$ 的分布贡献

• 状态分布差异分析：计算可得 $\vert p_{\theta}(s_t)-p_{train}(s_t)\vert=(1-(1 - \epsilon)^t)\vert p_{mistake}(s_t)-p_{train}(s_t)\vert\leq2(1-(1 - \epsilon)^t)$，利用恒等式 $(1 - \epsilon)^t\geq1 - \epsilon t$（当 $\epsilon\in[0,1]$ 时），进一步推出 $2(1-(1 - \epsilon)^t)\leq2\epsilon t$，这表明随着时间步 $t$ 的增加，以及犯错概率界限 $\epsilon$ 的影响，学习到的策略对应的状态分布 $p_{\theta}(s_t)$ 与训练集状态分布 $p_{train}(s_t)$ 的差异有一个逐渐增大的上界

期望形式推导

• 假设设定：假设学习到的策略 $\pi_{\theta}$ 与专家策略 $\pi^*$ 存在差异，在训练分布 $p_{train}(s)$ 下，策略 \pi_{\theta} 采取非专家动作（即与 $\pi^*(s)$ 不同的动作）的期望概率存在上界 $\epsilon$，即 $\mathbb{E}_{s \sim p_{train}(s)}[\pi_{\theta}(a \neq \pi^*(s)|s)] \leq \epsilon$，该式表明，平均来看，在训练阶段常见的状态下，策略 $\pi_{\theta}$ 偏离专家策略的程度是有限的，$\epsilon$ 刻画了这种偏离程度的上限

• 推导过程：设 $p_{\pi_{\theta}}(s_t)$ 和 $p_{train}(s_t)$ 分别为测试阶段和训练阶段在时间步 $t$ 的状态分布。通过概率论相关知识及推导，可以得到 $\mathbb{E}[\vert p_{\pi_{\theta}}(s_t) - p_{train}(s_t) \vert] \leq \epsilon$，直观理解，由于策略 $\pi_{\theta}$ 与专家策略的差异导致了状态分布的变化，而在上述假设下，训练与测试状态分布差异的期望被限制在 $\epsilon$ 以内 。这意味着，平均而言，测试阶段的状态分布与训练阶段状态分布不会相差太远，但随着时间推移或任务复杂性增加，这种差异仍可能对智能体性能产生影响

行为克隆的误差累积问题

（一）误差产生原因

1. 策略偏差：专家数据有限，无法覆盖所有情况；学习算法本身局限，不能完美拟合专家策略。

2. 分布偏移：训练和测试状态分布不同，导致智能体按训练策略行动产生误差并累积。

（二）误差影响

1. 性能退化：在连续任务中，误差累积使智能体表现逐渐变差。

2. 增加任务失败风险：可能使智能体进入错误且难以恢复的状态。

（三）缓解方法

1. 数据增强：对训练数据进行变换，扩充数据多样性。

2. 在线学习与更新：智能体在运行中持续学习新数据更新策略。

3. 多专家学习：融合多个专家策略，弥补单一专家局限性。

Goal-conditional 行为克隆

Goal-conditional Behavior Cloning 是模仿学习的一种扩展形式，它不仅学习如何模仿专家的动作，还考虑了目标条件：在标准行为克隆中，策略学习映射 $\pi(a|s)$，而在目标条件行为克隆中，策略学习映射 $\pi(a|s,g)$，其中 $g$ 表示目标

当目标是达到最终状态 $s_T$ 时，训练目标函数可以表示为：

我们希望最大化在当前状态 $s_t$ 下，给定目标 $g=s_T$（即最终状态）时，执行动作 $a_t$ 的对数概率

算法步骤：

1. 数据收集：收集包含状态、动作和目标三元组 $(s, a, g)$ 的专家示范数据集 $D$

2. 模型设计：构建模型 $\pi_\theta(a|s,g)$，该模型接收状态 $s$ 和目标 $g$ 作为输入，输出动作分布参数

3. 目标函数：通常使用最大似然估计作为训练目标

4. 优化过程：使用随机梯度上升或其变体来优化参数 $\theta$

5. 验证评估：在测试环境中使用不同目标来评估学习策略的性能

https://arxiv.org/abs/1906.05838

直接模仿有效果吗？

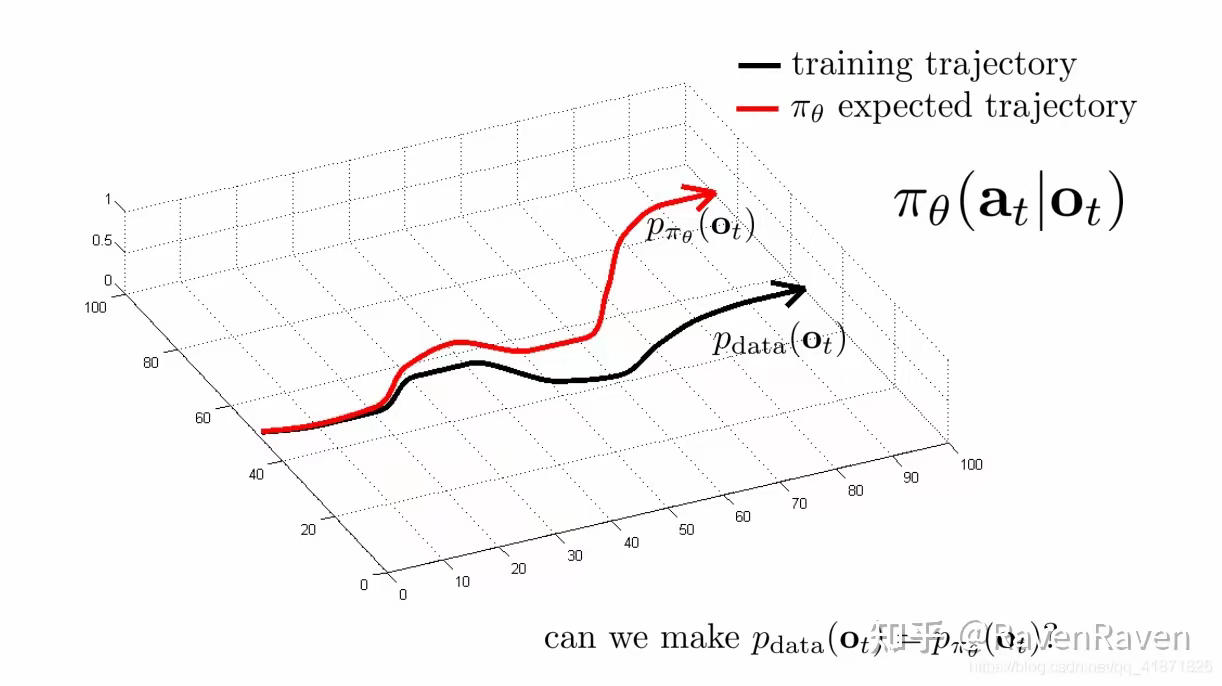
没有！为什么呢？模仿学习是一个 image classification 问题，我们都知道 classification network 训练后是有误差的；另外，模仿学习还是一个 sequence decision 问题，也就是当前时刻的决策会影响下一时刻的决策。我们用上图来解决为什么直接模仿没有效果。黑色轨迹指训练样本的 state 与时间的关系，红色是指用训练后的 policy 对训练样本进行测试后得到的轨迹。按理说，我们期望两者能重叠，但是，由于任何训练都是有误差的，这个误差一开始很小，导致 agent 看到了训练集没有的样本，虽然 deep network 有一定泛化能力，我们的 agent 还是走偏了一点。随着不断积累，agent 看到了越来越多的陌生样本，导致它完全偏离黑色轨迹。这就是模仿学习的“偏移”问题。这个问题根源是：sequence decision 问题的因果关联和样本分布不够广泛

核心的思路是收集更多有用的数据，从而提高模仿学习的效果

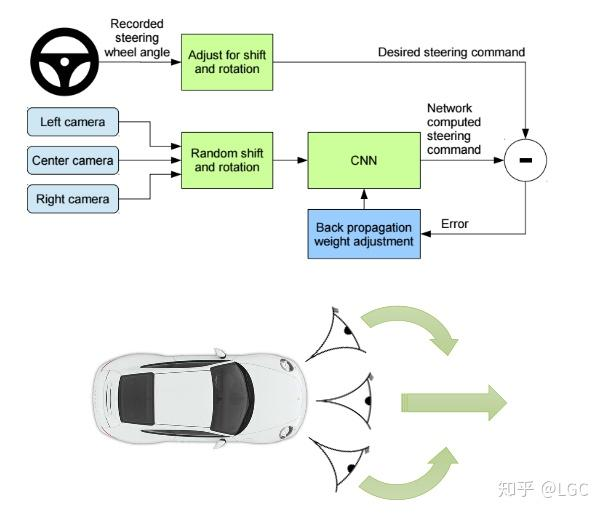
数据多样化

如果只用中间相机采集数据进行训练，训练后的网络容易让汽车“偏移”车道。为了解决这个问题，作者增加了左、右两个相机，采集汽车左右两侧的图像，左图像对应的指令是右转，右图像是左转

DAgger: Dataset Aggregation

之前的方法都是改变/优化策略，通过减少错误来使 $p_{\pi_\theta}(o_t)$ 接近 $p_{data}(o_t)$

为了解决复合误差问题，Stéphane Ross 等人又提出了 DAgger(Dataset Aggregation)算法。这是一个基 于在线学习的算法，其把行为克隆得到的策略与环境不断的交互，来产生新的数据。在 这些新产生的数据上，DAgger 会向专家策略申请示例；然后在增广后的数据集上，DAgger 会重新使用行为克隆 进行训练，然后再与环境交互；这个过程会不断重复进行。由于数据增广和环境交互，DAgger 算法会大大减小未访问的状态的个数，从而减小误差

为什么有时候不能很好地拟合专家数据

非马尔科夫行为 Non-Markovian behavior

马尔科夫属性是指当前事件的发生与过去事件无关。在模仿学习中，我们通常使用：$\pi_\theta(a_t|o_t) \quad$

但在实际中，我们很可能需要利用过去的观测值来预测接下来的行为：$\pi_\theta(a_t|o_1,...,o_t) \quad$

利用历史数据可能会让模仿学习模型的性能更差，因为它会加剧"causal confusion"（因果混淆）

https://proceedings.neurips.cc/paper/2019/hash/947018640bf36a2bb609d3557a285329-Abstract.html

多模态行为 Multimodal behavior

多模态行为指在相同状态下可能存在多种合理但不同的行动方式。例如，绕过一棵树可以向左走也可以向右走，但向前走会撞树。

对于离散动作，这不存在问题。但对于连续动作，如果从单一高斯分布采样，很可能产生中间的无效动作（如撞树）。

解决方法：

1. 高斯混合模型：让网络输出 N 个高斯模型组成混合模型，从中采样获得最优动作

2. 隐变量模型：通过引入隐变量捕获行为多样性

3. 自回归离散化：首先把动作的第 1 维离散为多个动作，采样得到第 1 个最优动作；然后将第 1 个动作和图像作为第 2 个网络的输入，输出第 2 个最优动作；以此类推