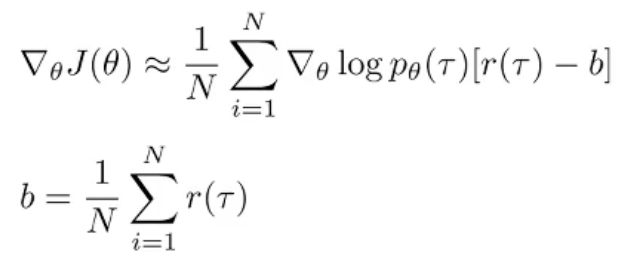
请解释什么是 Policy Gradient?【Policy Gradient 是一种直接优化策略函数 π(a∣s) 的强化学习方法。它通过神经网络直接输出动作概率分布,然后使用梯度上升来优化期望回报】
目标函数
在真实环境下运行策略 πθ 收集 n 个采样轨迹:
- si,t: 第 i 个样本在 t 个时间步的状态
- ai,t: 第 i 个样本在 t 个时间步的动作
- ri,t: 第 i 个样本在 t 个时间步获得的奖励
假设已经收集了 n 个采样轨迹 τi=(si,1,ai,1,ri,1,si,2,ai,2,ri,2,...),其中包含状态、动作和奖赏
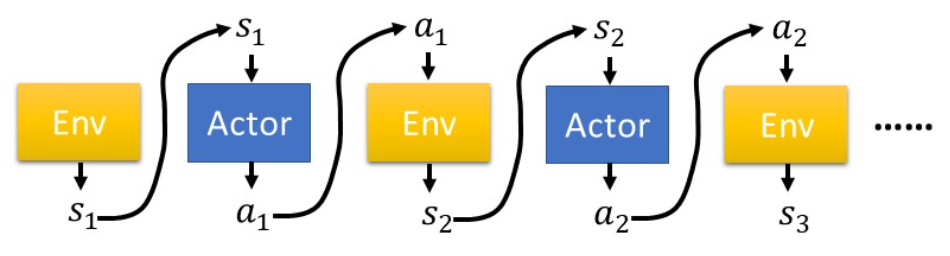
我们可以将累积奖赏的期望值表示为:
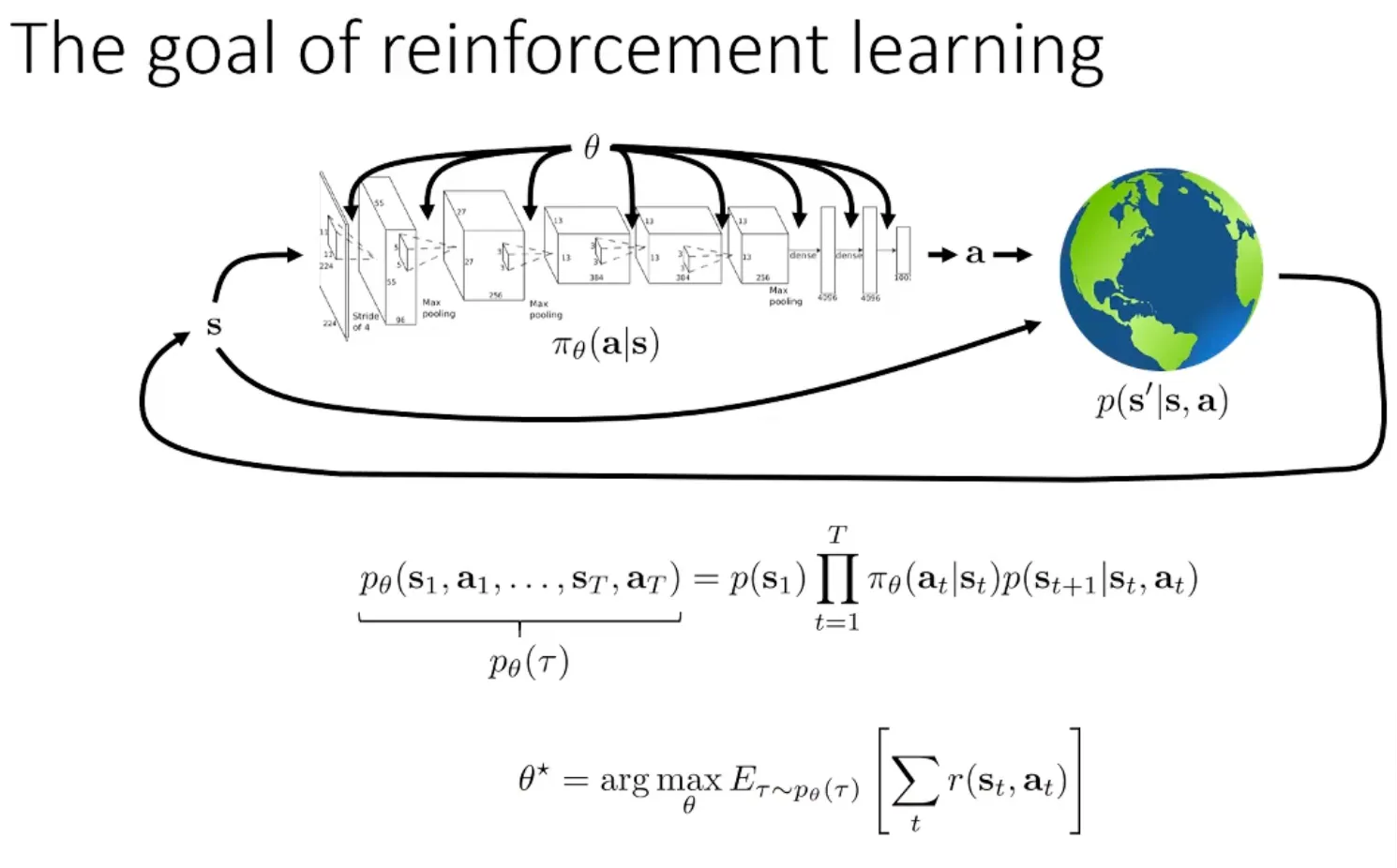
J(θ)=Eτ∼Pθ(τ)[t=1∑∞r(st,at)]=τ∑R(τ)Pθ(τ) - R(τ) 表示轨迹 τ 的累积奖赏
- Pθ(τ) 表示在参数 θ 下产生轨迹 τ 的概率
Pθ(τ) 可以进一步展开为:
Pθ(τ)=P(s1)πθ(a1∣s1)P(s2∣s1,a1)πθ(a2∣s2)P(s3∣s2,a2)...=P(s1)t=1∏Tπθ(at∣st)P(st+1∣st,at) - 其中 P(st+1∣st,at) 是由环境所决定的
Policy Gradient 的目的在于找到一组最优参数 θ∗,使得上述期望值最大值
θ∗=argmaxτ∑R(τ)Pθ(τ) 无偏估计
由于无法直接计算 J(θ),我们可以采用无偏估计
J(θ)≈N1i∑t∑r(si,t,ai,t) 通过将样本轨迹上的奖励相加,然后进行平均,得到总奖励期望的无偏估计
使用蒙特卡洛采样要计算期望:E[f(x)]=∫f(x)p(x)dx
- 从分布 p(x) 中采样 N 个样本:x1,x2,...,xN
- 计算均值:E[f(x)]≈N1∑i=1Nf(xi)
数学推导
现在我们已经知道:
R(τ)=t=1∑Tr(st,at)Pθ(τ)=P(s1)t=1∏T(πθ(at∣st)P(st+1∣st,at))J(θ)=τ∑R(τ)Pθ(τ) 以及对数求导恒等式(逆用):
∇f(x)=f(x)∇logf(x)pθ(τ)∇θlogpθ(τ)=pθ(τ)pθ(τ)∇θpθ(τ)=∇θpθ(τ) 求 ∇J(θ):
∇J(θ)=∇τ∑R(τ)Pθ(τ)=τ∑R(τ)∇Pθ(τ)=τ∑R(τ)Pθ(τ)∇logPθ(τ)=Eτ∼Pθ(τ)[R(τ)∇logPθ(τ)] 由 Pθ(τ)=P(s1)∏t=1T(Pθ(at∣st)P(st+1∣st,at)) 可知:
logPθ(τ)=logP(s1)+t=1∑Tlogπθ(at∣st)+t=1∑TlogP(st+1∣st,at) - 其中 logP(s1) 和 ∑t=1TlogP(st+1∣st,at) 这两项与 θ 无关!
所以:
∇J(θ)=Eτ∼Pθ(τ)[R(τ)∇logPθ(τ)]=Eτ∼Pθ(τ)[R(τ)∇t=1∑Tlogπθ(at∣st)]=Eτ∼Pθ(τ)[t=1∑Tr(st,at)t=1∑T∇logπθ(at∣st)] 这个期望内的所有东西都是已知的,都能够访问
实际计算时采用无偏估计:
∇J(θ)≈N1i=1∑N(t=1∑T∇logπθ(ati∣sti)t=1∑Tr(sti,ati)) Policy Gradient 定理中的期望是关于轨迹的,为什么最终可以转化为关于单步动作的期望?【这是因为马尔可夫性质和概率分解,求导后状态转移项消失(与 θ 无关)】
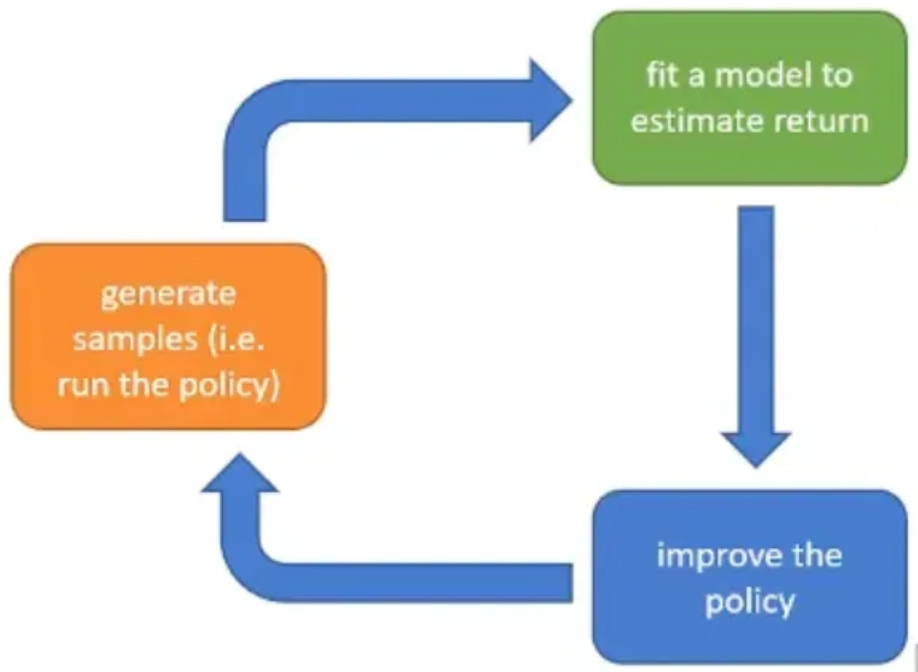
实际上 REINFORCE 算法就是通过这种方式计算的:
- Sample τi from πθ(at∣st) (run the policy)
- ∇J(θ)≈N1∑i=1N(∑t=1T∇logπθ(ati∣sti)∑t=1Tr(sti,ati))
- θ←θ+α∇J(θ)
式子中的梯度表明了增加轨迹 τ 概率的方向,可以看到式子中的 πθ(τi) 与奖励值相乘,从直观上来理解,Policy Gradient 使得好的事情更有可能发生,使得坏的事情更不可能发生【试错学习】
高方差问题
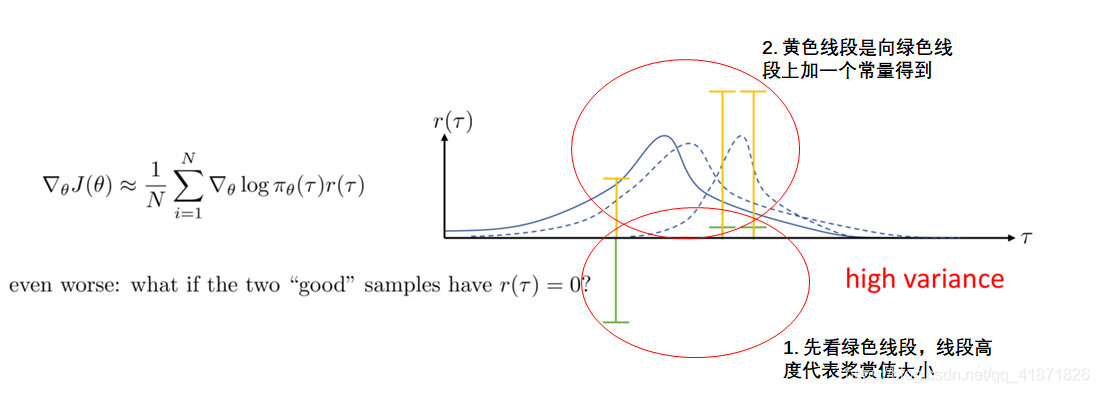
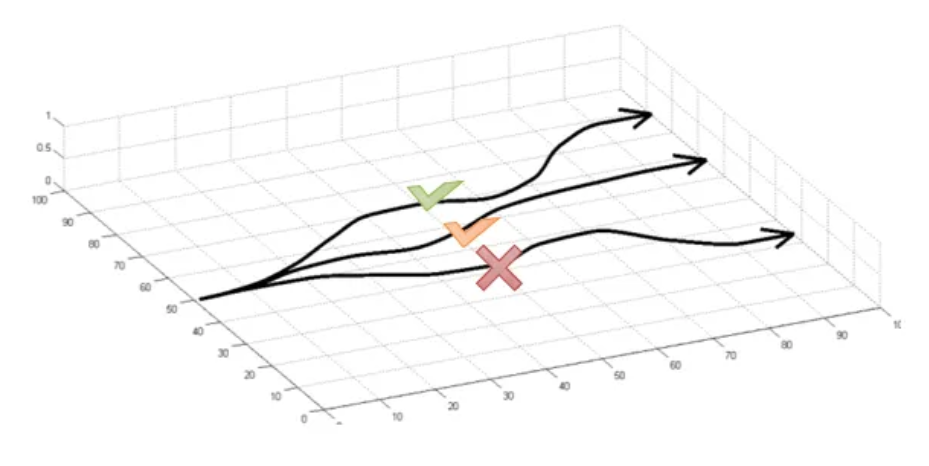
横轴 τ 表示不同的采样轨迹,纵轴 r(τ) 表示对应的奖励值,蓝色曲线表示策略分布
- 绿色竖线代表两个采样轨迹获得的奖励值(对于较高奖励的轨迹,下一次采样的概率分布会向其偏移,同时,策略会试图远离低奖励的轨迹)
虽然加入常量不会影响策略梯度的理论计算,但会导致了两次采样得到显著不同的概率分布。这直观地展示了策略梯度的高方差问题 - 即使是细微的奖励变化都可能导致策略更新的不稳定性。
降低高方差
Causality 假设
该假设认为未来时刻的策略选择并不能影响当前及之前时刻得到的奖赏。
因此,在计算当前动作的梯度时,只需考虑从当前时刻开始往后推移获得的奖赏,而不需要考虑之前的奖赏
优点:有助于去除与当前决策无关的噪声,从而降低梯度估计的方差
加入 Baseline
非常有用!!!
将奖励值减去平均奖励,就像给奖励一个参考系:直观地理解,Baseline告诉我们在状态 s 下平均可以获得多少奖励,它提供了一个参考点(归一化)。如果某个动作的奖励高于平均水平,我们就增加其概率;反之则降低其概率
Off-policy & 重要性采样
Policy Gradient 是一种典型的 on-policy 算法,每次修改策略时都需要新的样本,每次采样的数据在一次梯度上升之后就被扔掉了
理论上来说,on-policy 的算法只能使用当前正在优化的 policy 生成的数据来进行训练
为什么每次需要新的样本?【对策略参数 θ 求导需要根据 θ 采样的样本,当策略从 θ 更新到 θ′ 时,样本分布也发生了改变。继续使用旧数据估计新策略的梯度会导致偏差,因此必须丢弃之前的样本】
在使用深度神经网络作为策略函数近似器时,由于神经网络的高度非线性,所以不能采用大梯度更新,因此每次更新只能使用小批量数据进行小幅度更新,这就需要大量的更新步骤,每一步都需要从当前策略采样新数据。当样本生成成本较高时,这会带来巨大的采样开销
为了提高样本利用效率,一种可能的解决方案是使用重要性采样将 on-policy 算法转化为 off-policy
重要性采样引入了重要性权重 ρt=πθ(at∣st)πθ′(at∣st) 来修正行为策略 πθ 和目标策略 πθ′ 之间的分布差异:
Policy Gradient 方法的实现技巧
总体上只需要给出损失函数即可,剩下的任务交给 pytorch 去做
其他要点:
- 使用较大的 batch size 对参数进行更新,几千
- 手动调整 learning_rates 很困难,可以使用 ADAM 优化器