深度强化学习 Intro

PPO 里面的 GAE 是怎么算的？代表了什么？

✏️极大似然估计

https://www.bilibili.com/video/BV1iz421h7gb/?spm_id_from=333.337.search-card.all.click&vd_source=bd8e3cdb5bbacad892e151f2df59cf05

https://www.bilibili.com/video/BV1TQ4y1v7H5/?spm_id_from=333.337.top_right_bar_window_custom_collection.content.click&vd_source=bd8e3cdb5bbacad892e151f2df59cf05

目前，在可靠性（stability）和采样效率（sample efficiency）这两个关键因素上，PPO 和 SAC 是表现最优的策略学习算法

术语速查

概述

https://rail.eecs.berkeley.edu/deeprlcourse/deeprlcourse/static/slides/lec-1.pdf

Deep RL = Classical RL + Advanced optimization algorithm

• 深度，提供从大型数据集中进行可扩展学习的能力

• 强化，提供优化，即采取行动的能力

强化学习 v.s. 监督学习

RL 不只是能做游戏，机器人，还可以用来控制交通流量（MIT 教授），大语言模型，图像生成模型

核心思想：通过不断与环境交互，从经验中学习做出最优决策

方向：Learing-based control, which is a big open problem

奖励从哪里来？游戏（得分 easy）；倒水（？difficult）

人类学习的特殊性

• 能够在稀疏奖励环境中有效学习

• 例子：攻读博士学位
  • 最终奖励可能只有一次
  • 需要长期规划和持续投入，中间过程缺乏明确的奖励信号

如何去构建一个智能机器？

Leaning 是智能的基石，人理解世界的本质其实就是学习的过程

挑战

1. 缺少同时使用数据（深度）和优化（强化）的方法;

2. 人学得很快，而 deep RL 方法学得慢;

3. 人擅长复用知识，而 deep RL 很难在不同任务之间迁移;

4. 不清楚奖励函数应该是什么;

5. 不清楚预测的作用

MDPs 马尔可夫决策过程

马尔可夫链： $\mathcal{M} = \{\mathcal{S}, \mathcal{T}\}$

$\mathcal{S}$ - state space

$\mathcal{T}$ - transition operator, $p(s_{t+1}|s_{t})$

马尔可夫过程：$\mathcal{M} = \{\mathcal{S}, \mathcal{A}, \mathcal{T}, r\}$

$\mathcal{S}$ - state space

$\mathcal{A}$ - action space

$\mathcal{T}$ - transition operator, $p(s_{t+1}|s_{t})$

$r$ - reward function

部分可观察的马尔可夫过程：$\mathcal{M} = \{\mathcal{S}, \mathcal{A}, \mathcal{O}, \mathcal{T}, \mathcal{E}, r\}$

强化学习定义

通过从与环境交互过程中进行学习

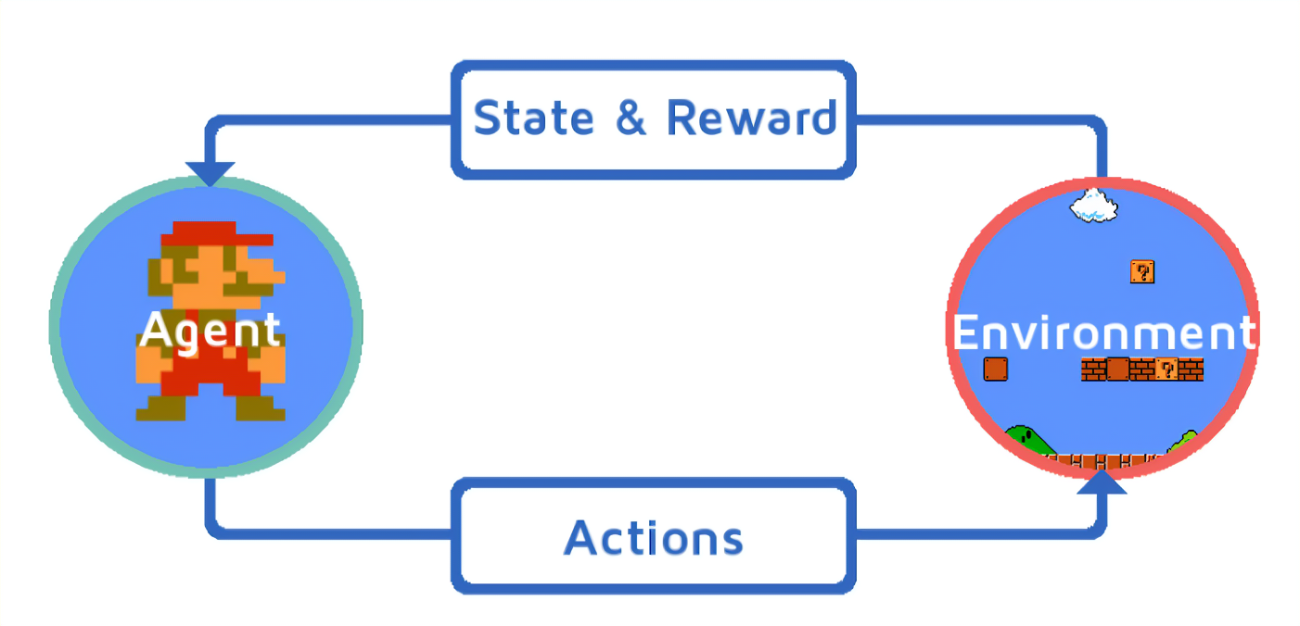
each step, agent obtains an observation, takes an action, and obtains a reward

强化学习的框架主要由以下几个核心组成：

• 状态（State）：反映 environment 当前的情况。

• 动作（Action）：智能体在特定状态下可以采取的操作。

• 奖励（Reward）：一个数值反馈，用于量化智能体采取某一动作后环境的反应。

• 策略（Policy）：一个映射函数，指导智能体在特定状态下应采取哪一动作。

  

这四个元素共同构成了马尔可夫决策过程（Markov Decision Process, MDP）最核心的数学模型。

注：MDPs 很好的一个性质：memoryless property 与历史无关

强化学习的目标是在给定的马尔可夫决策过程中找到最优策略。这个策略是从状态到动作的映射，旨在最大化累积回报，其数学表达式如下：

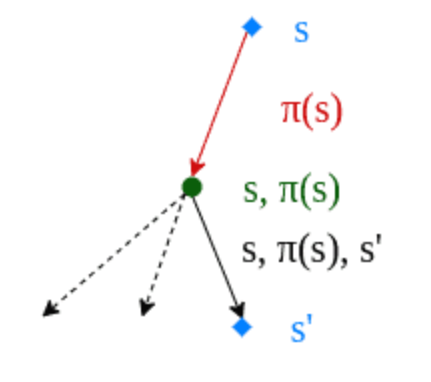
• 状态转移（State transition）：agent 执行某个动作，由一个状态变成另一个状态

• 累计回报奖励（Return）：$r_t = R_t + R_{t+1} + R_{t+2} + ...$
  • $R_t$ 和 $R_{t+1}$ 不是同等重要，这也是为什么会出现折扣因子
  • 折扣回报（Discounted return）：$r_t = R_t + \gamma R_{t+1} + \gamma ^ 2R_{t+2} + ...$

强化学习中的随机性

用期望把随机性积掉

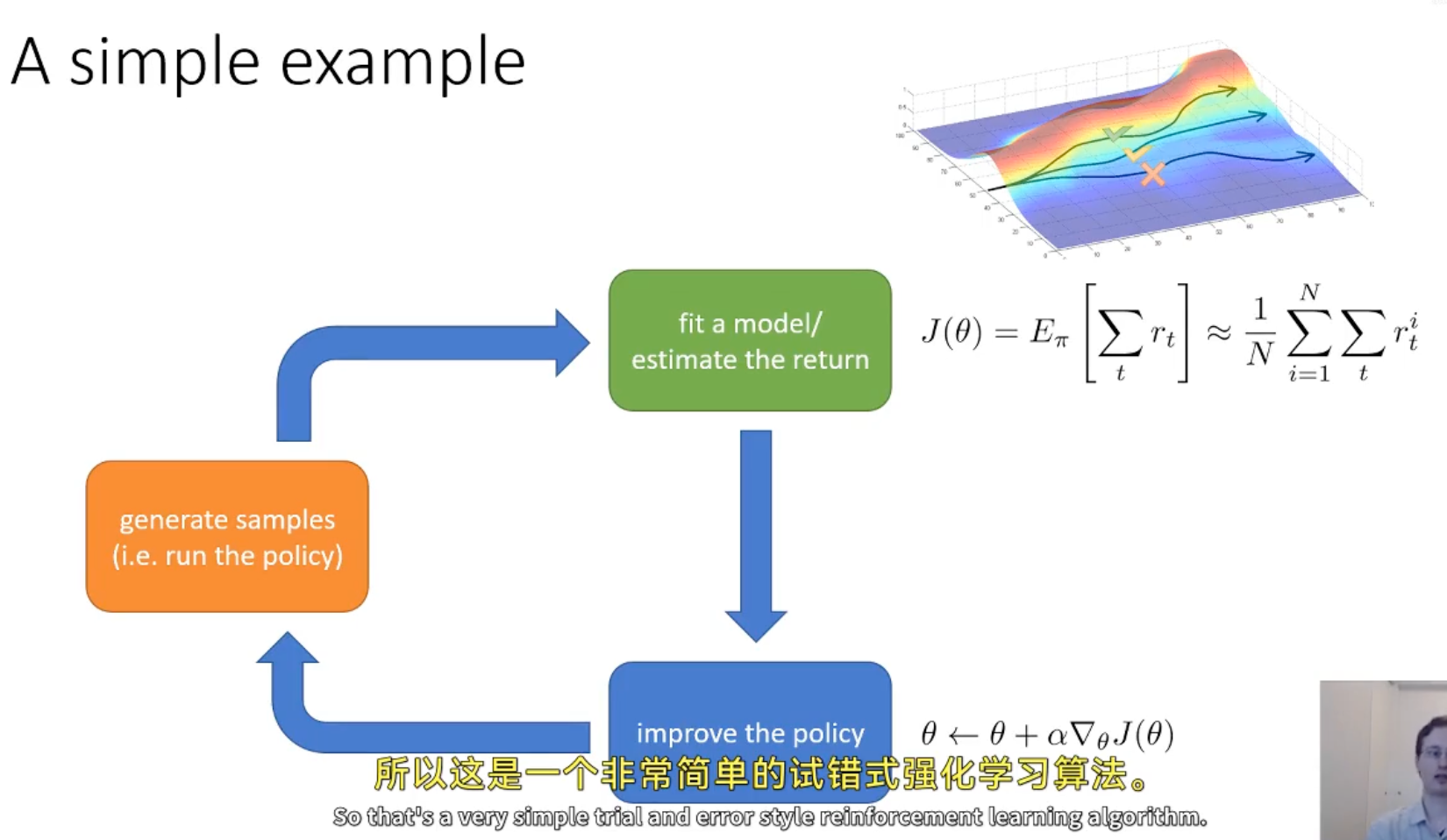
强化学习目标

策略优化的目标是最大化期望回报

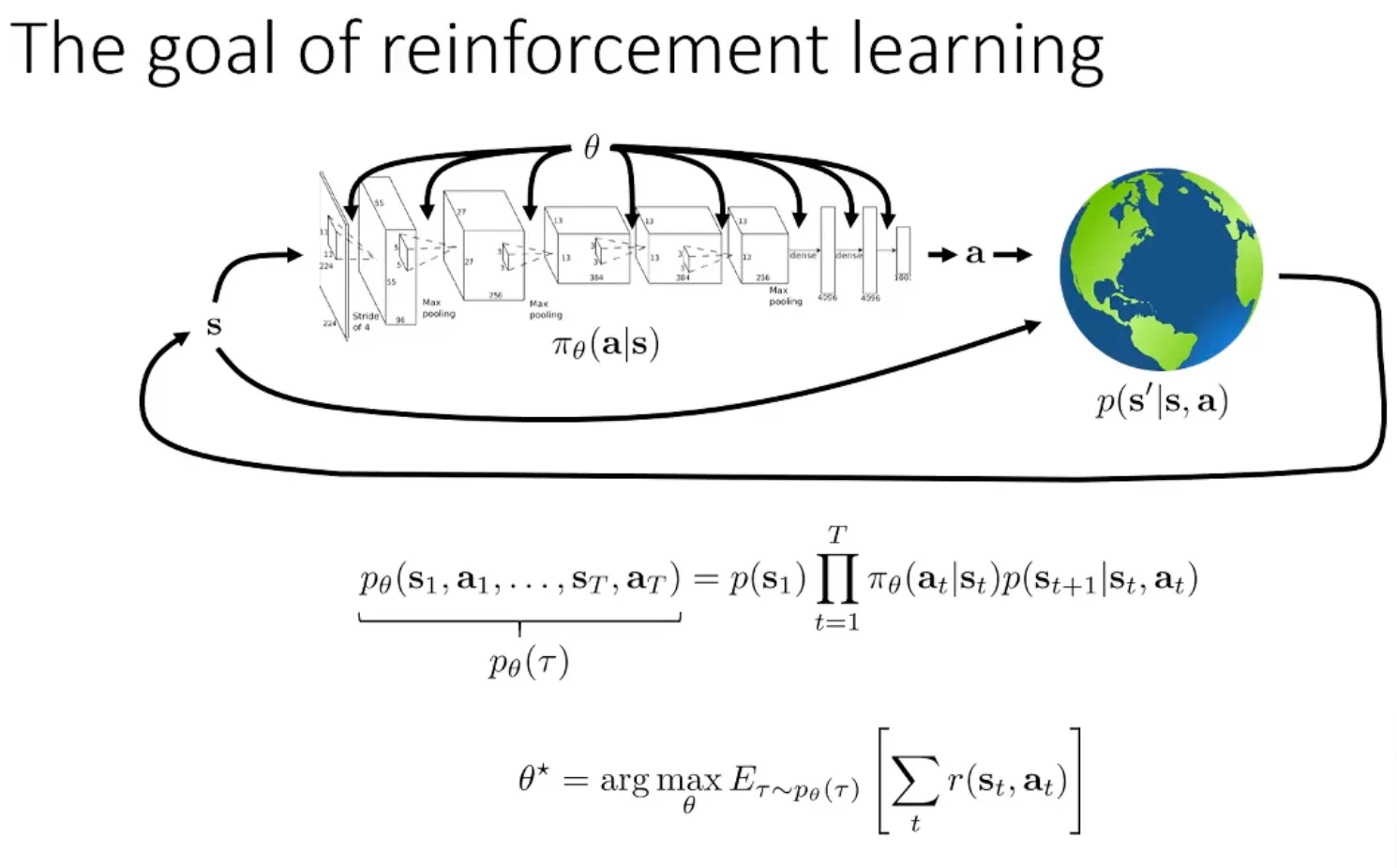
其中：

• $\theta$：策略参数

• $\tau$：轨迹

• $T$：时间步长

$\pi_{\theta}$ 中的 $\theta$ 表示我们需要学习的策略中的参数

状态 1 转换到状态 2 = 状态转移算子 * 策略

目标：某条轨迹分布下的奖励总和

当时间趋于无穷时，奖励总和趋于无穷，无法优化。解决方法：除以 ${T}$ 或者使用折扣因子

计算整个轨迹的奖励函数，然后使用梯度上升更新策略参数

通过神经网络来学习策略，然后使用反向传播来更新策略参数

期望

强化学习的目标：优化一个期望函数

Q 函数：在给定状态 $s$ 下采取特定动作 $a$ 后，所能够获得的长期回报（或累积奖励）的期望值

V 函数：在给定状态 $s$ 下的总体价值，即按照策略执行后续动作所能获得的长期回报的期望值

我们可以通过 Q 函数来改进策略：

1. 直接选最优动作：如果我们知道策略 $\pi$ 的 Q 函数 $Q^\pi(s, a)$，就可以在每个状态 $s$ 下选择收益最高的动作 $a$。假设 $\pi'(a|s) = 1$，若 $a = \arg\max_a Q^\pi(s, a)$ ，那么可以知道新策略的效果至少与原策略一样好，甚至更优。（为什么会更优？）

2. 调整概率倾向于好动作：如果直接选最优动作不现实，可以通过增加收益高于平均值的动作的概率来改进策略。当 $Q^\pi(s, a) > V^\pi(s)$ 时，说明该动作比平均收益高，我们就提高其选择概率，从而让策略逐渐倾向于选择“好动作”。

greedy 方法：每次都选择最大 value 对应的 action，即 $a = \arg\max_a Q^\pi(s, a)$

Q / V function

Q-function 叫做动作价值函数；V-function 叫做状态价值函数

• 对于一个 policy $\pi$，$Q_{\pi}(s,a)$ 用来评估 agent 在状态 $s$ 采取动作 $a$ 是否合适

• 对于一个固定的 policy $\pi$，$V_{\pi}(s)$ 用来评估状态 $s$ 的好坏
  • $\mathbb{E}_S[V_\pi(S)]$ 用来评估策略 $\pi$ 的好坏

如何控制 agent

学到 policy $\pi(a|s)$ 或 $Q^*(s,a)$ 两者之一即可

强化学习算法分类

• Policy gradients
  • 直接优化策略函数，通过策略的梯度来更新策略参数
  • REINFORCE, TRPO (Trust Region Policy Optimization), PPO (Proximal Policy Optimization)

• Value-based
  • 通过学习状态 Q 函数或 V 函数来间接选择动作（隐式）
  • 基于神经网络来估计 Q 函数
  • Q-learning, DQN

• Actor-critic：结合 Policy Gradients 和 Value-Based 方法
  • 神经网络来拟合模型去估计回报（Value-based），梯度上升去更新参数（Policy gradients）
  • Actor：更新策略（Policy），生成动作；Critic：评估动作的质量（Value），给出反馈
  • A3C (Asynchronous Advantage Actor-Critic), SAC (Soft Actor-Critic)

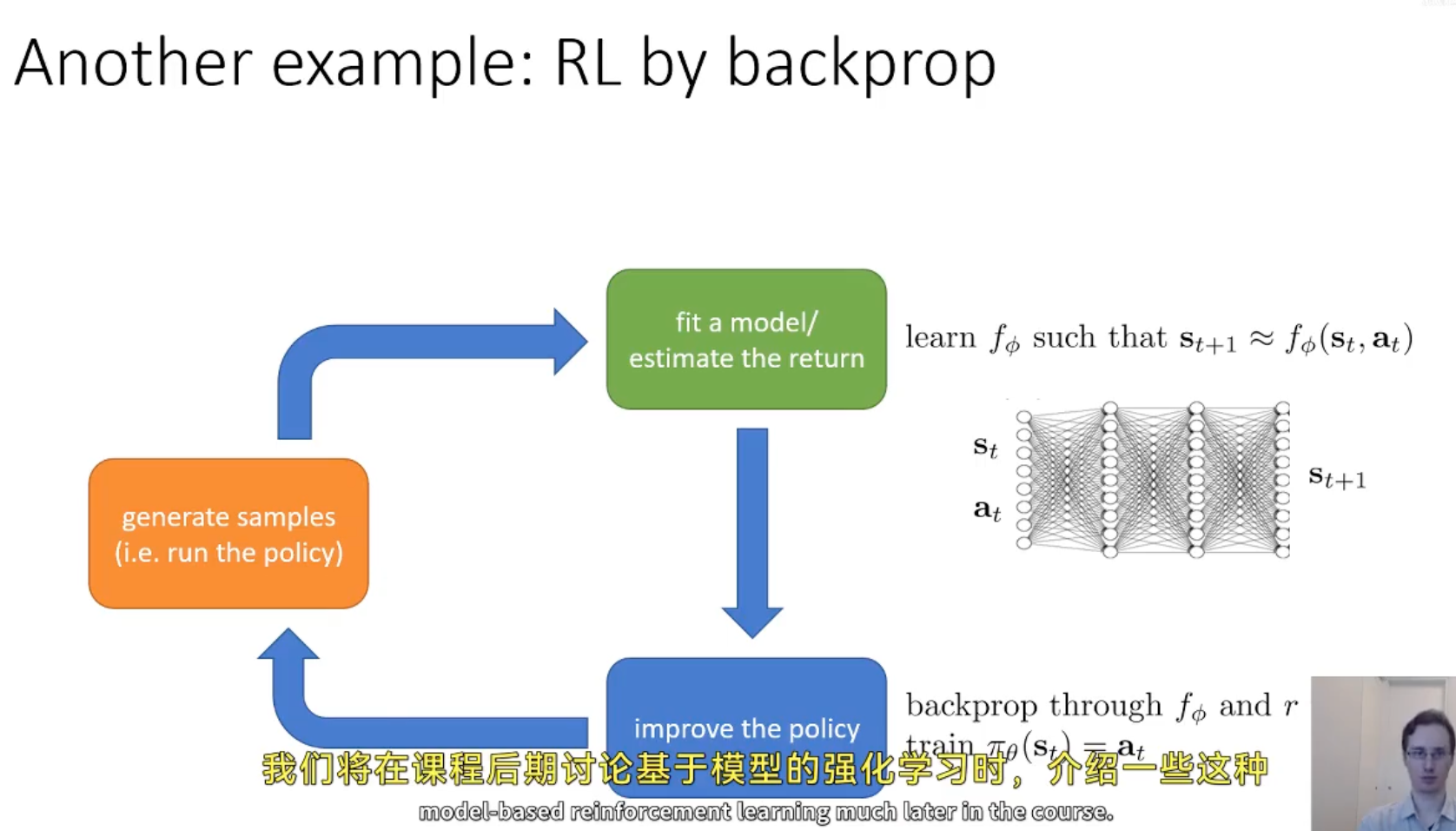
• Model-based RL：显式建模环境的动态转移模型，用于规划或模拟
  • learn $P(s_{t+1}, a_t)$

算法评估维度

采样效率：需要多少样本来获得一个表现良好的策略

稳定性和易用性：是否震荡？能否收敛？

• Value-based：最好情况下，能够最小化拟合损失；最坏情况下，完全不能拟合

• Model-based：一定能收敛，但不保证收敛的模型就是最好的模型

• Policy gradient：唯一真正直接优化目标，效率最低

观测可用性：全观测还是部分观测

On-Policy v.s. Off-Policy

On-Policy 特点：

1. 不使用历史数据，在采样效率上表现较差；

2. 直接优化策略表现（即以采样效率换取可靠性）；

3. 之后提出的 On-Policy 算法都是在不断弥补采样效率的不足

Policy Gradient → TRPO → PPO

Off-Policy 特点：

1. 典型算法：Q-Learning 和 DDPG → TD3 → SAC

2. 通过对 Bellman 方程的优化，实现对历史数据的有效利用；

3. 问题：满足 Bellman 方程并不能保证一定有很好的策略性能，不稳定（从经验上讲，满足 Bellman 方程能得到不错的性能、很好的效率）。TD3 和 SAC 是基于 DDPG 进行改进，在一定程度上有效缓解了这些问题

为什么 less efficient 算法还存在？采样效率快的算法在实际应用中可能会面临更高的计算成本

基于学习的策略

按照学习目标划分：基于策略（Policy-Based）和基于价值（Value-Based）

• Policy-Based方法直接输出下一步动作的概率分布，并根据此分布选择动作。然而，它不一定选择概率最高的动作，而是会从整体角度考虑。这种方法适用于连续和离散的动作空间。典型代表是Policy Gradients算法。

• Value-Based方法输出每个动作的价值估计，并选择价值最高的动作。这种方法主要适用于离散动作空间。常见算法包括Q-learning、Deep Q Network和Sarsa。

• 更高级的方法是结合上述两种approach：Actor-Critic。在这种方法中，Actor根据概率分布选择动作，Critic评估动作的价值，从而加速学习过程。代表算法有A2C、A3C和DDPG等。

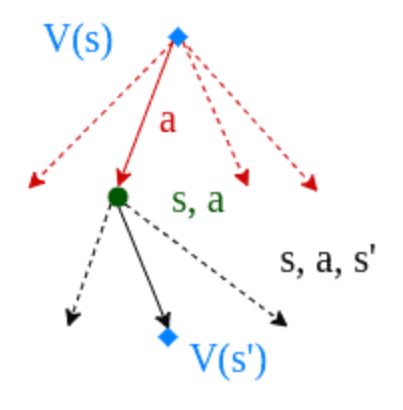
与策略迭代相比，价值迭代不考虑不同动作的概率，而是直接选择价值最高的动作

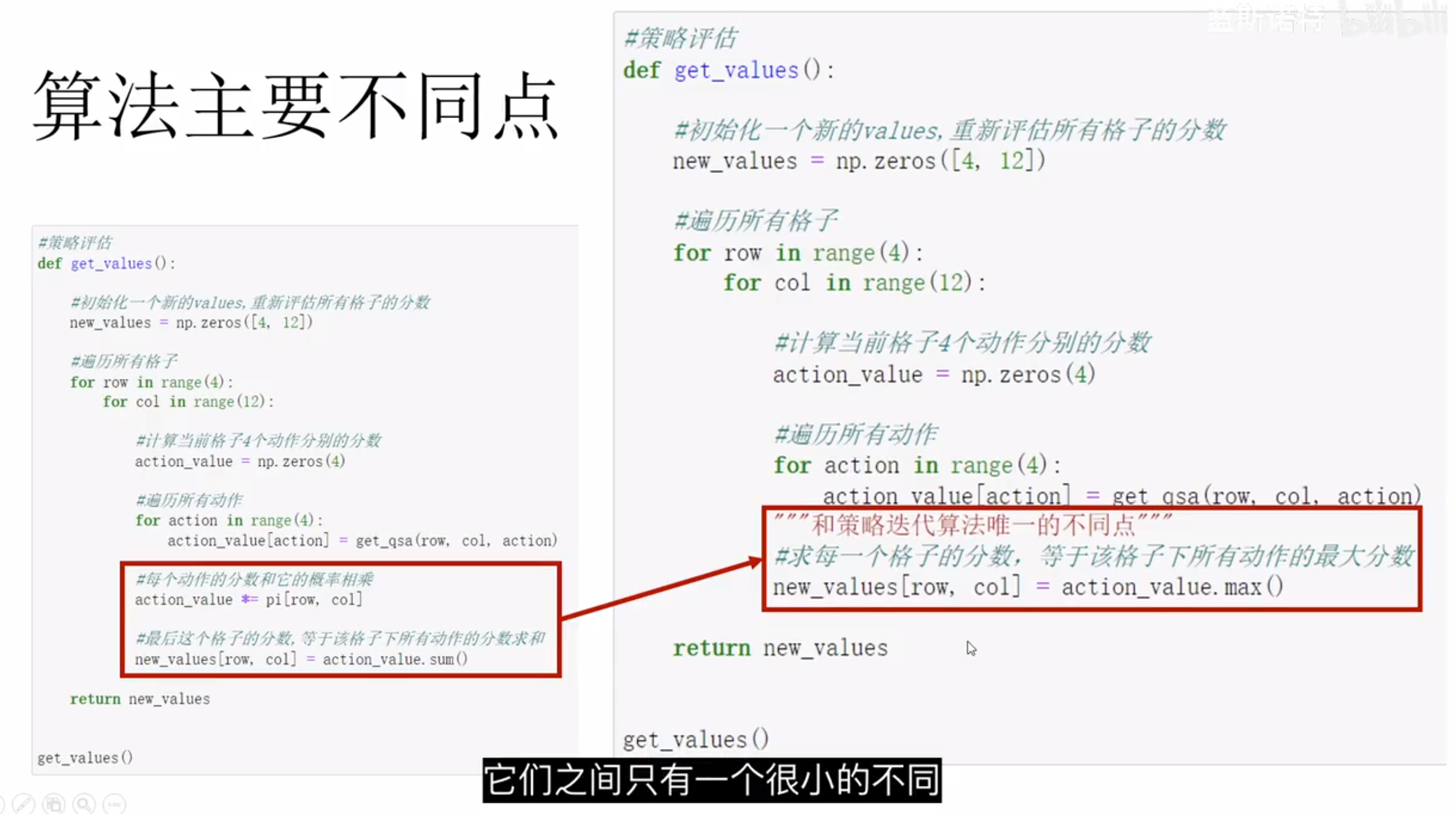
https://www.baeldung.com/cs/ml-value-iteration-vs-policy-iteration

Policy iteration

Value iteration