机器人学中的姿态的表示方法

“运动是相对的。”

让我们想想，达成同一个变换的结果，比如把点 (1,1)(1,1) 变到点 (2,3)(2,3) 去，你可以有两种做法。第一，坐标系不动，点动，把 (1,1)(1,1)点挪到 (2,3)(2,3) 去。第二，点不动，变坐标系，让 x 轴的度量（单位向量）变成原来的 1/2，让 y 轴的度量（单位向量）变成原先的 1/3，这样点还是那个点，可是点的坐标就变成 (2,3)(2,3) 了。方式不同，结果一样。

从第一个方式来看，那就是我在《理解矩阵》1/2 中说的，把矩阵看成是运动描述，矩阵与向量相乘就是使向量（点）运动的过程。在这个方式下，Ma=bMa=b 的意思是：“向量 aa 经过矩阵 MM 所描述的变换，变成了向量 bb。”

而从第二个方式来看，矩阵 MM 描述了一个坐标系，姑且也称之为 MM。那么：Ma=bMa=b 的意思是：

“有一个向量，它在坐标系 MM 的度量下得到的度量结果向量为 aa，那么它在坐标系 II 的度量下，这个向量的度量结果是 bb。”

这里的 II 是指单位矩阵，就是主对角线是 1，其他为零的矩阵。

而这两个方式本质上是等价的。

欧拉角、姿态角、四元数、旋转矩阵、方向余弦矩阵、轴角

在空间中如何表示一个刚体的状态
zhuanlan.zhihu.com
https://zhuanlan.zhihu.com/p/67305147

Rotation Matrix

BAR^A_BR： 左上角 AA 表示基准坐标系，坐标系 BB 相对于坐标系 AA

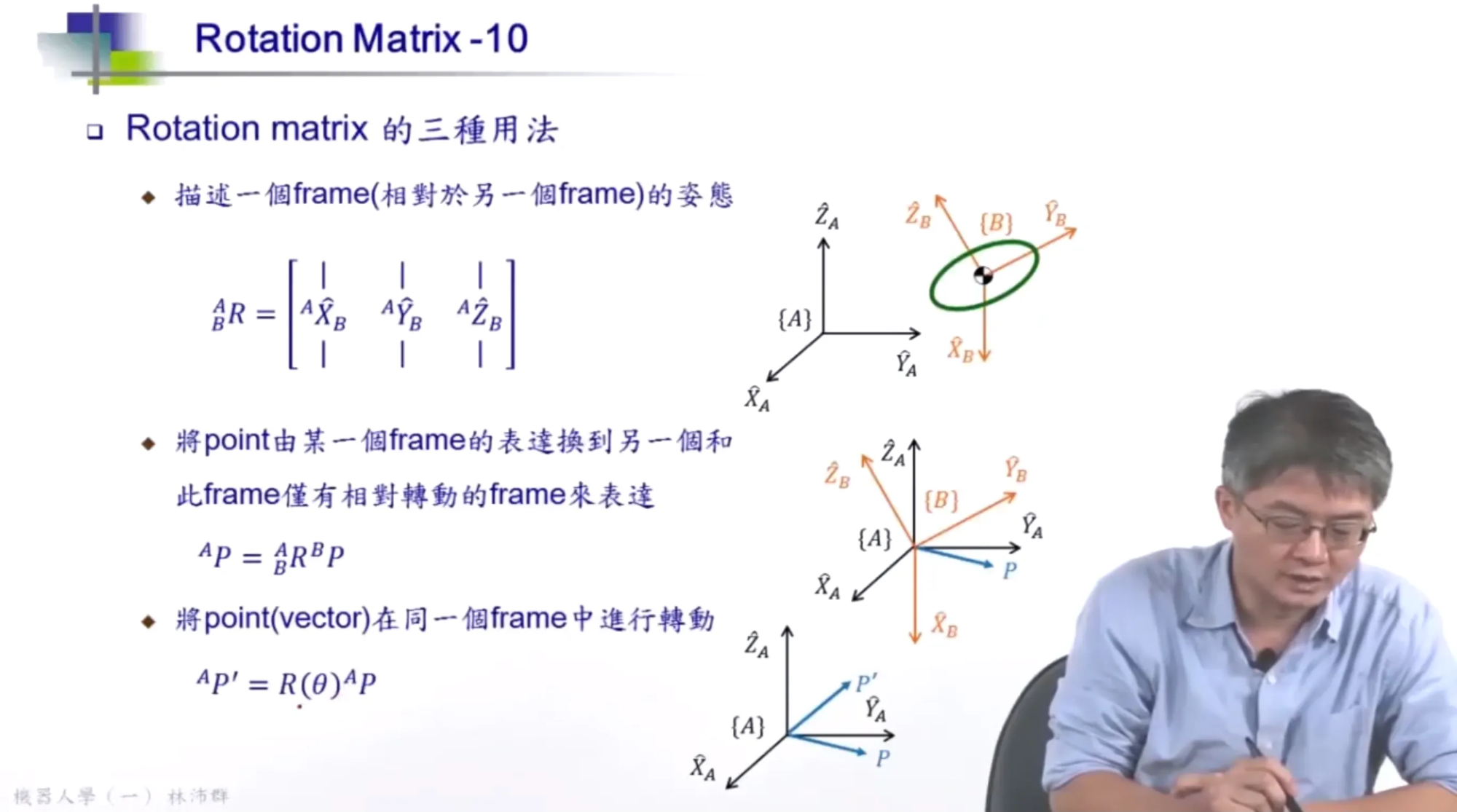
表示三维旋转的旋转矩阵 RR 是一个 3×33 \times 3，行列式为 1 的正交矩阵，也就是说它的每个列向量都是单位向量，每两个列向量互相正交（垂直）。

Fixed Angles

x, y, z 三个轴固定，依次旋转

从左到右：绕 XAX_A 旋转，绕 YAY_A 旋转，绕 ZAZ_A 旋转

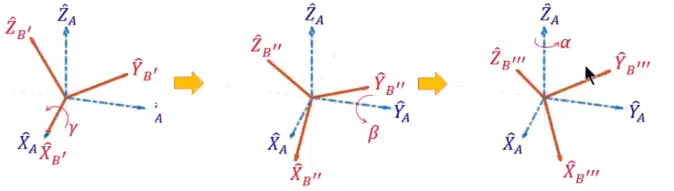
  1. 由 angles 推算 RR
BARXYZ(γ,β,α)=RZ(α)RY(β)RX(α)^A_BR_{XYZ}(\gamma, \beta, \alpha) = R_Z(\alpha)R_Y(\beta)R_X(\alpha)

特点：先转放右边，后转放左边 v′= BARv=R3R2R1vv' =~ ^A_BR v = R_3R_2R_1 v

注：更换转动顺序后，旋转矩阵值与末姿态都不相同，即若转动角度相同，顺序不同，最终状态不同

BARXYZ(γ,β,α)=RZ(α)RY(β)RX(γ)=[cos⁡α−sin⁡α0sin⁡αcos⁡α0001][cos⁡β0sin⁡β010−sin⁡β0cos⁡β][1000cos⁡γ−sin⁡γ0sin⁡γcos⁡γ]\begin{align} ^A_BR_{XYZ}(\gamma, \beta, \alpha) &= R_Z(\alpha)R_Y(\beta)R_X(\gamma) \\ &= \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{bmatrix} \end{align}
  1. 由 RR 推算 angles
BARXYZ(γ,β,α)=[r11r12r13r21r22r23r31r32r33]\begin{align} ^A_BR_{XYZ}(\gamma, \beta, \alpha) &= \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{bmatrix} \end{align}

解出 γ,β,α\gamma, \beta, \alpha

Euler Angles

欧拉角大概是最常用到的姿态表示方法了，它的思路是把一个三维旋转分解为三个绕坐标轴的旋转。欧拉角使用时最令人困惑的地方在于它的不同定义方法：根据三个坐标轴的不同顺序，可以有 12 种定义方法；根据坐标轴是惯性坐标系（extrinsic）还是体坐标系（intrinsic），可以有 2 种定义方法。因此，一共有 24 种可能的方法来定义欧拉角，而且这些定义方式没有一种是通用的，因此每次使用欧拉角时一定要说明是哪种定义。

个人理解，这里所说的绕惯性坐标系的旋转，也被称为 fixed angles

转动轴不固定，绕被转动转轴去做旋转

从左到右：先根据 ZBZ_B 转，再根据 YBY_B 转，最后根据 XBX_B 转

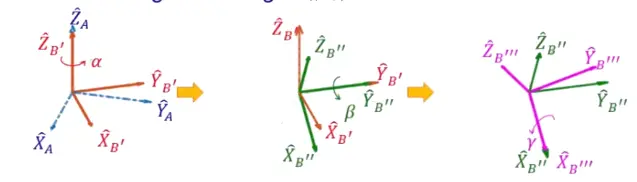
  1. 由 angles 推算 RR【Z-Y-X】
BARZ′Y′X′(α,β,γ)=RZ′(α)RY′(β)RX′(α)^A_BR_{Z'Y'X'}(\alpha, \beta, \gamma) = R_{Z'}(\alpha)R_{Y'}(\beta)R_{X'}(\alpha)

特点：先转放左面，后转放右面

BARZ′Y′X′(α,β,γ)=RZ′(α)RY′(β)RX′(γ)=[cos⁡α−sin⁡α0sin⁡αcos⁡α0001][cos⁡β0sin⁡β010−sin⁡β0cos⁡β][1000cos⁡γ−sin⁡γ0sin⁡γcos⁡γ]\begin{align} ^A_BR_{Z'Y'X'}(\alpha, \beta, \gamma) &= R_{Z'}(\alpha)R_{Y'}(\beta)R_{X'}(\gamma) \\ &= \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{bmatrix} \end{align}

实际上 BARZ′Y′X′(α,β,γ)= BARXYZ(γ,β,α)^A_BR_{Z'Y'X'}(\alpha, \beta, \gamma) =~ ^A_BR_{XYZ}(\gamma, \beta, \alpha)

XYZ Fixed Angles 和 ZYX Euler Angles 的比较
zhuanlan.zhihu.com
https://zhuanlan.zhihu.com/p/28325851?utm_psn=1832196155464900609

注：更换转动顺序后，旋转矩阵值与末姿态都不相同，即若转动角度相同，顺序不同，最终状态不同

  1. 由 RR 推算 angles【Z-Y-Z】

Quaternions

定义：q=s+xi+yj+zk  s,x,y,z∈Rq = s + {x}i + {y}j + {z}k~~ s,x,y,z \in \mathbb{R}

三个虚数单位服从以下运算规则

  1. i2=j2=k2=−1i^2=j^2=k^2=-1
  1. ij=k,jk=i,ki=jij=k, jk=i, ki=j

三维旋转可以用单位四元数表示，即 ∣∣q∣∣=qw2+qx2+qy2+qz2=1||\textbf{q}||=\sqrt{q_w^2+q_x^2+q_y^2+q_z^2}=1

Summary

单位四元数可以通过旋转矢量 uθ 来表示三维旋转：

q=[cos⁡(θ/2),sin⁡(θ/2)ux,sin⁡(θ/2)uy,sin⁡(θ/2)uz]q = [\cos(\theta/2), \sin(\theta/2)u_x, \sin(\theta/2)u_y, \sin(\theta/2)u_z]

将 θ=−θ,u=−u\theta = -\theta, u = -u 代入上式得到 -q\textbf{-q}，说明 qq 和 −q-q 表示相同的三维旋转。这是单位四元数的重要性质：它与三维旋转是 2 比 1 的对应关系，而非一一对应。

在四种表示方法中：旋转矢量和欧拉角使用三个参数；四元数使用四个参数和一个约束条件（长度为1）；旋转矩阵使用九个参数和六个约束条件（矩阵的正交性）。旋转矢量和欧拉角在某些姿态下会出现奇异性，导致其导数趋向无穷大。四元数没有奇异性，但与姿态是 2 比 1 的对应关系。只有旋转矩阵既无奇异性，又与姿态一一对应。

Homogeneous transformation matrix

整合表达刚体的状态：把平动和转动用一个矩阵表示

在刚体（Rigid body）上建立 frame，常建立在质心上

  1. 平动：由 body frame 的原点位置判定
  1. 转动：由 body frame 的姿态判定
T=[Rp01]=[r11r12r13p1r21r22r23p2r31r32r33p30001](1)T=\left[\begin{array}{ll} R & p \\ 0 & 1 \end{array}\right]=\left[\begin{array}{llll} r_{11} & r_{12} & r_{13} & p_{1} \\ r_{21} & r_{22} & r_{23} & p_{2} \\ r_{31} & r_{32} & r_{33} & p_{3} \\ 0 & 0 & 0 & 1 \end{array}\right] \tag{1}
  1. 对平动复合
  1. 对转动复合
  1. 同时平动转动

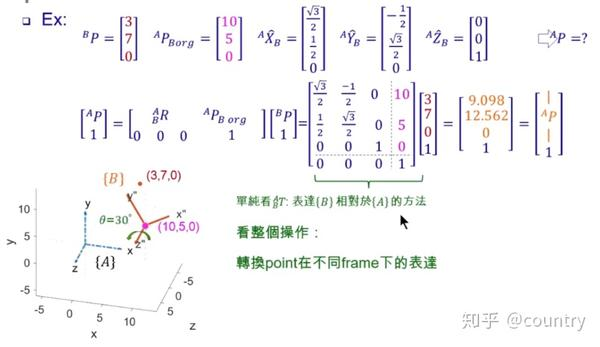
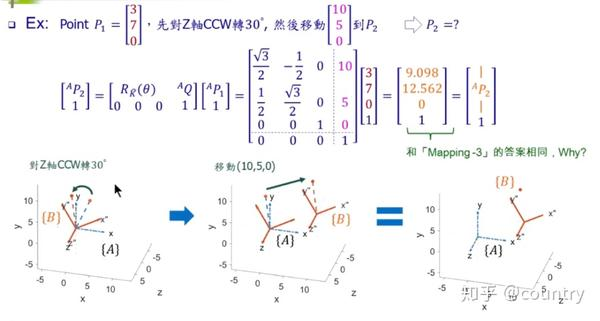
原因：旋转矩阵一致，位移矩阵一致，当然一样

齐次变换矩阵的三种用法

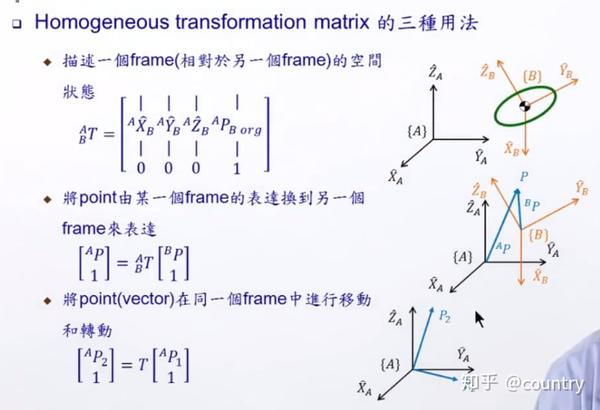
连续运算法则

premultiply 左乘 固定轴

postmultiply 右乘